Cosa hanno in comune le Piramidi di Giza e la Gioconda di Da Vinci con Twitter e Pepsi? Risposta rapida: sono tutti progettati utilizzando la sezione aurea.
La sezione aurea è una proporzione matematica. Si trova comunemente in natura e, se utilizzato in un design, favorisce composizioni organiche e dall’aspetto naturale che sono esteticamente piacevoli alla vista.
Ma qual è la sezione aurea?
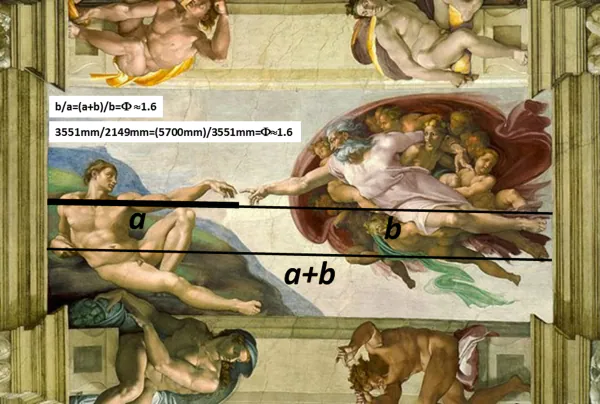
In parole povere, la sezione aurea (nota anche come media aurea, proporzione divina o lettera greca Phi φ) esiste quando una linea è divisa in due parti e la parte più lunga (a) divisa per la parte minore (b) è uguale alla somma di (a) + (b) divisa per (a), che equivalgono entrambi a 1,618.
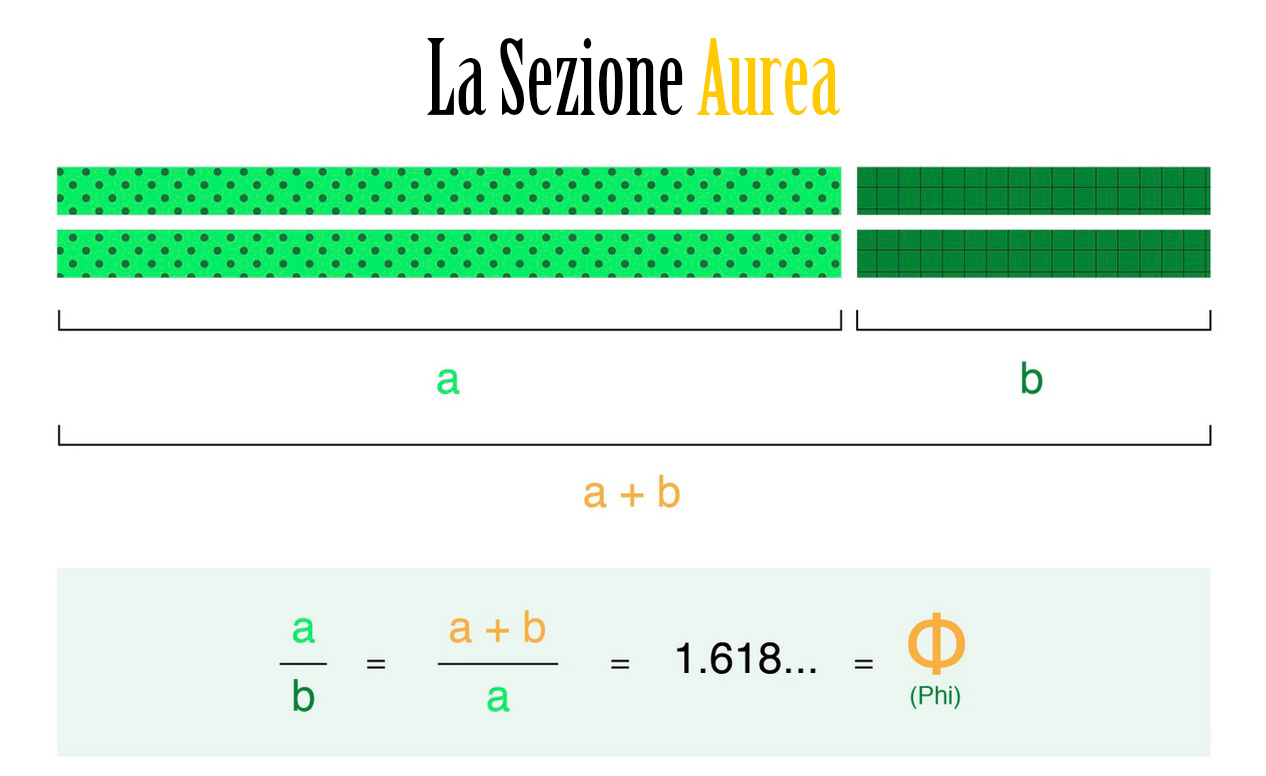
Ma non lasciarti abbattere da tutta la matematica.
Nel design, la sezione aurea si riduce all’estetica per creare e apprezzare un senso di bellezza attraverso l’armonia e la proporzione
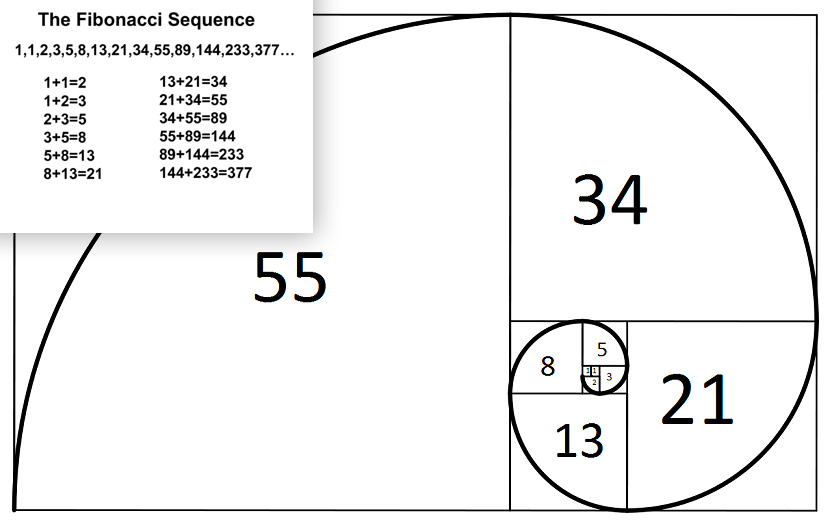
Non si può parlare di Sezione Aurea senza includere anche nel discorso la sequenza di Fibonacci.
La connessione fra i numeri di Fibonacci e la sezione aurea venne verificata nel XIX secolo: se ogni numero di Fibonacci viene diviso per quello precedente, man mano che avanziamo
nella sequenza il risultato ottenuto tende a φ cioè si avvicina progressivamente alla sezione aurea.
Quando applicato al design, la sezione aurea fornisce un senso artistico; un fattore X; un certo je ne sais quoi.
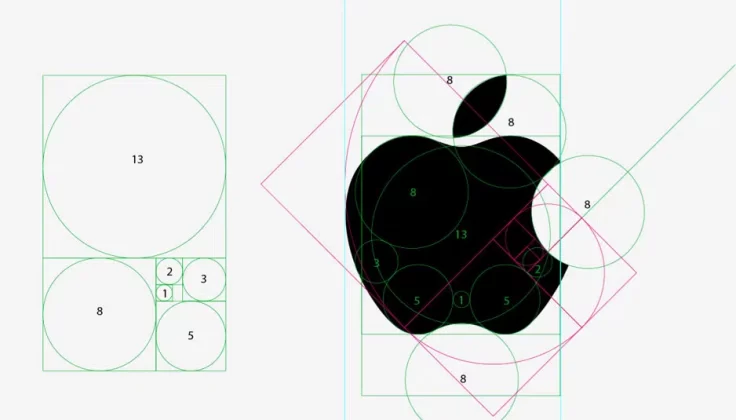
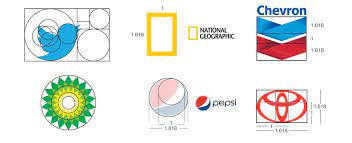
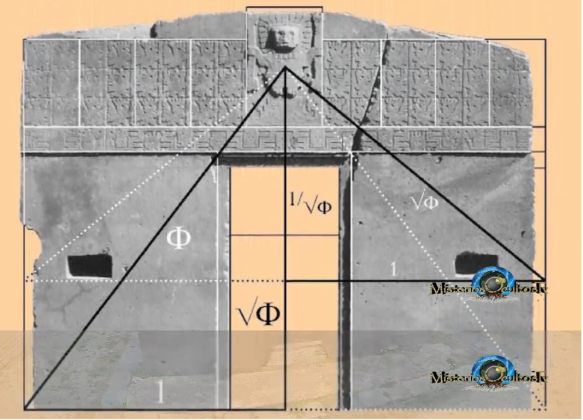
Questa armonia e proporzione è stata riconosciuta per migliaia di secoli: dalle Piramidi di Giza al Partenone di Atene; Michelangelo Creazione di Adamo di sul soffitto della Cappella Sistina alla Gioconda di Da Vinci; perfino la Porta del Sole di Tiahuanaco risalente a oltre il 1500 a.C., (La Paz, Bolivia) fino ai moderni loghi delle più grandi aziende come Pepsi, Apple ecc…
Anche Leonardo da Vinci aveva approfondito questo aspetto matematico, evidente nel disegno dell’uomo vitruviano e nella maggioranza dei suoi dipinti: in essi le proporzioni seguono il rapporto aureo, mentre la composizione del soggetto e dell’inquadratura si realizzano mediante il rettangolo aureo, basato sullo stesso principio.
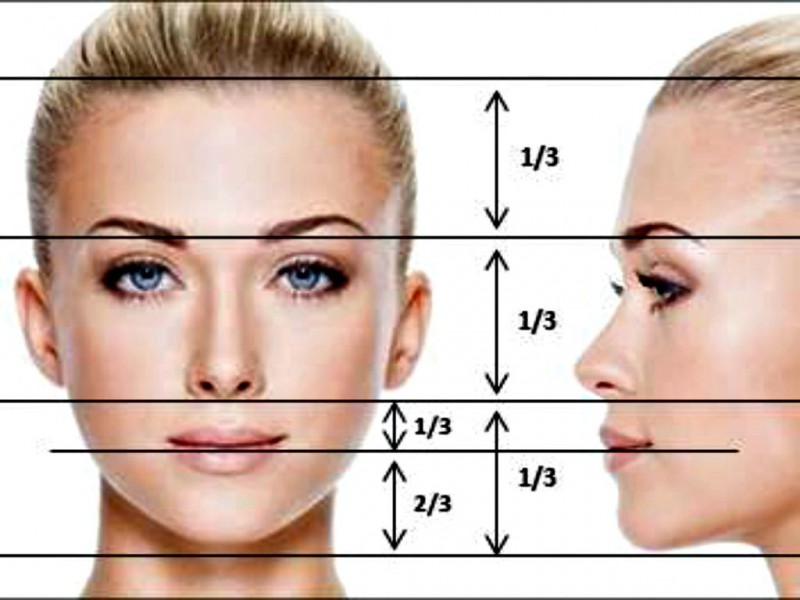
Anche i nostri corpi e i nostri volti seguono anche il rapporto matematico: In effetti, i nostri cervelli sono apparentemente programmati per preferire oggetti e immagini che utilizzano la sezione aurea. È quasi un’attrazione subconscia e anche piccoli ritocchi che rendono un’immagine più fedele alla sezione aurea hanno un grande impatto sul nostro cervello.
La bocca e il naso sono posizionati ciascuno in sezioni auree della distanza tra gli occhi e la parte inferiore del mento. Proporzioni simili possono essere viste di lato, e persino l’occhio e l’orecchio stesso seguono le proporzioni a spirale.
Vale la pena notare che il corpo di ogni persona è diverso, ma che le medie tra le popolazioni tendono al phi. È stato anche detto che più le nostre proporzioni aderiscono a phi, più “attraenti” sono percepiti quei tratti. Ad esempio, i sorrisi più “belli” sono quelli in cui gli incisivi centrali sono 1.618 più larghi degli incisivi laterali, che sono 1.618 più larghi dei canini, e così via. È del tutto possibile che, dal punto di vista evo-psicologico, siamo pronti ad apprezzare le forme fisiche che aderiscono alla sezione aurea, un potenziale indicatore di idoneità riproduttiva e salute.
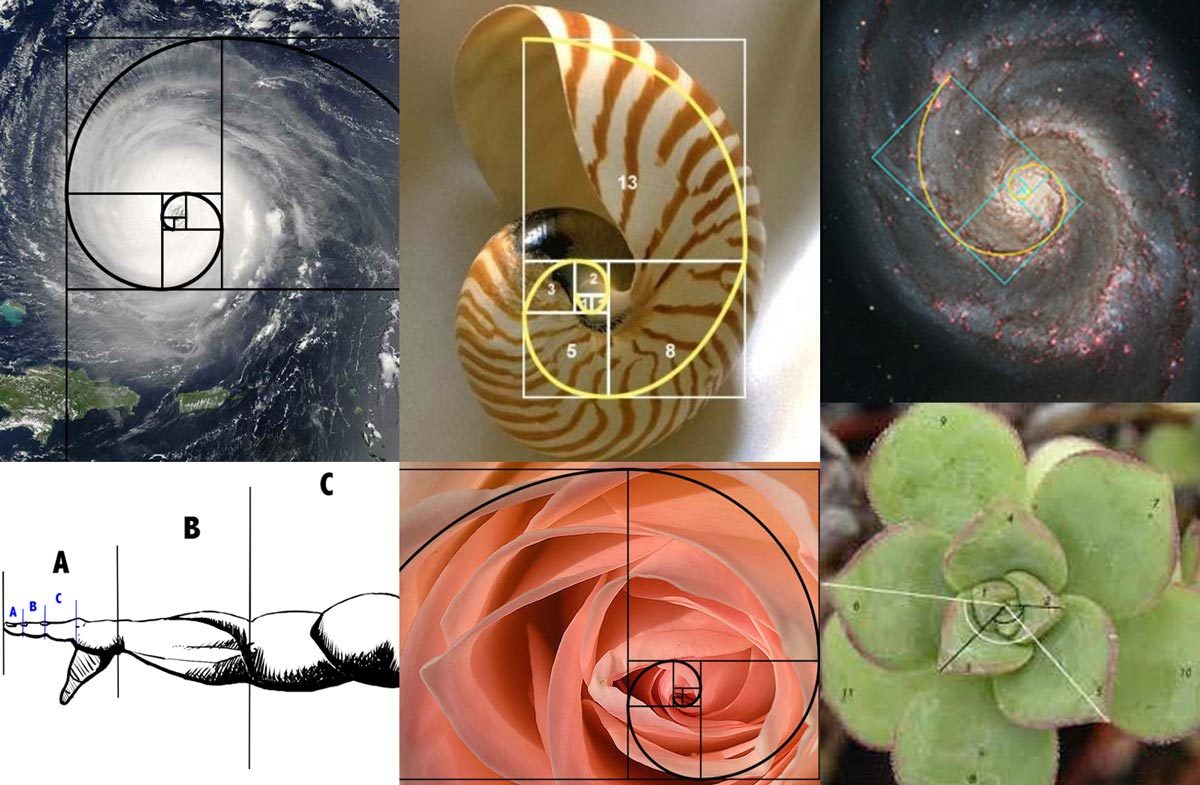
Troverai la sezione aurea in tutte le forme della natura – felci, fiori, conchiglie e persino uragani ecco perché troviamo la natura così bella e straordinaria.
In effetti, i migliori esempi di serie di Fibonacci nel mondo reale si trovano nel regno vegetale. Molte piante che si ramificano verso l’esterno verso il sole lo fanno in rami uguali ai numeri di Fibonacci. Il rametto originale esce dalla terra. Per il primo periodo, germoglia semplicemente verso l’alto. Quindi sviluppa punti di meristema – punti da cui possono formarsi nuovi rami – e quelli germogliano in due rami separati. Quei rami si spingono verso l’alto per un altro periodo di tempo, quindi sviluppano due punti propri. Il numero complessivo di punti di germogliamento si sviluppa in una serie di Fibonacci.
L’esempio più celebre della serie di Fibonacci sono le spirali che crea.
Cimette su un cavolfiore, frutticini su un ananas, semi su un girasole, tutti a spirale verso l’esterno. E ciascuna di queste spirali contiene un numero di semi, fiori, protuberanze, foglie o tubercoli che sono uguali a un numero di Fibonacci. Alcuni potrebbero dire che gli esseri umani scelgono e scelgono, decidendo d’ignorare i fiori che non producono i loro semi in una serie di Fibonacci, ma si scopre che c’è una ragione per i numeri di Fibonacci ripetuti su diverse specie di piante a spirale: è il modo perfetto per pacchetto.
Quando un bulbo di girasole sviluppa semi, deve dare a ciascuno dei suoi potenziali discendenti lo stesso spazio per fiorire. Devono essere imballati nel modo più uniforme e uniforme possibile. Ma le spirali non sono il modo migliore per inserire i semi in uno spazio, quindi perché le piante lo fanno? Perché non costruiscono uno spazio e poi lo riempiono di semi come fanno gli umani in un magazzino. Fanno semi mentre il bulbo in cui maturano quei semi si espande.
Il mistero della forma delle galassie
Non sorprende che anche le galassie a spirale seguano il familiare modello di Fibonacci. La Via Lattea ha diversi bracci a spirale, ognuno dei quali è una spirale logaritmica di circa 12 gradi. Un aspetto interessante è che le galassie a spirale sembrano sfidare la fisica newtoniana. Già nel 1925, gli astronomi si resero conto che, poiché la velocità angolare di rotazione del disco galattico varia con la distanza dal centro, i bracci radiali dovrebbero diventare curvi mentre le galassie ruotano. Successivamente, dopo alcune rotazioni, i bracci a spirale dovrebbero iniziare ad avvolgersi attorno a una galassia. Ma non lo fanno, da qui il cosiddetto problema dell’avvolgimento. Sembrerebbe che le stelle all’esterno si muovano a una velocità superiore al previsto, un tratto unico del cosmo che aiuta a preservarne la forma.
Dal macrocosmo al microcosmo
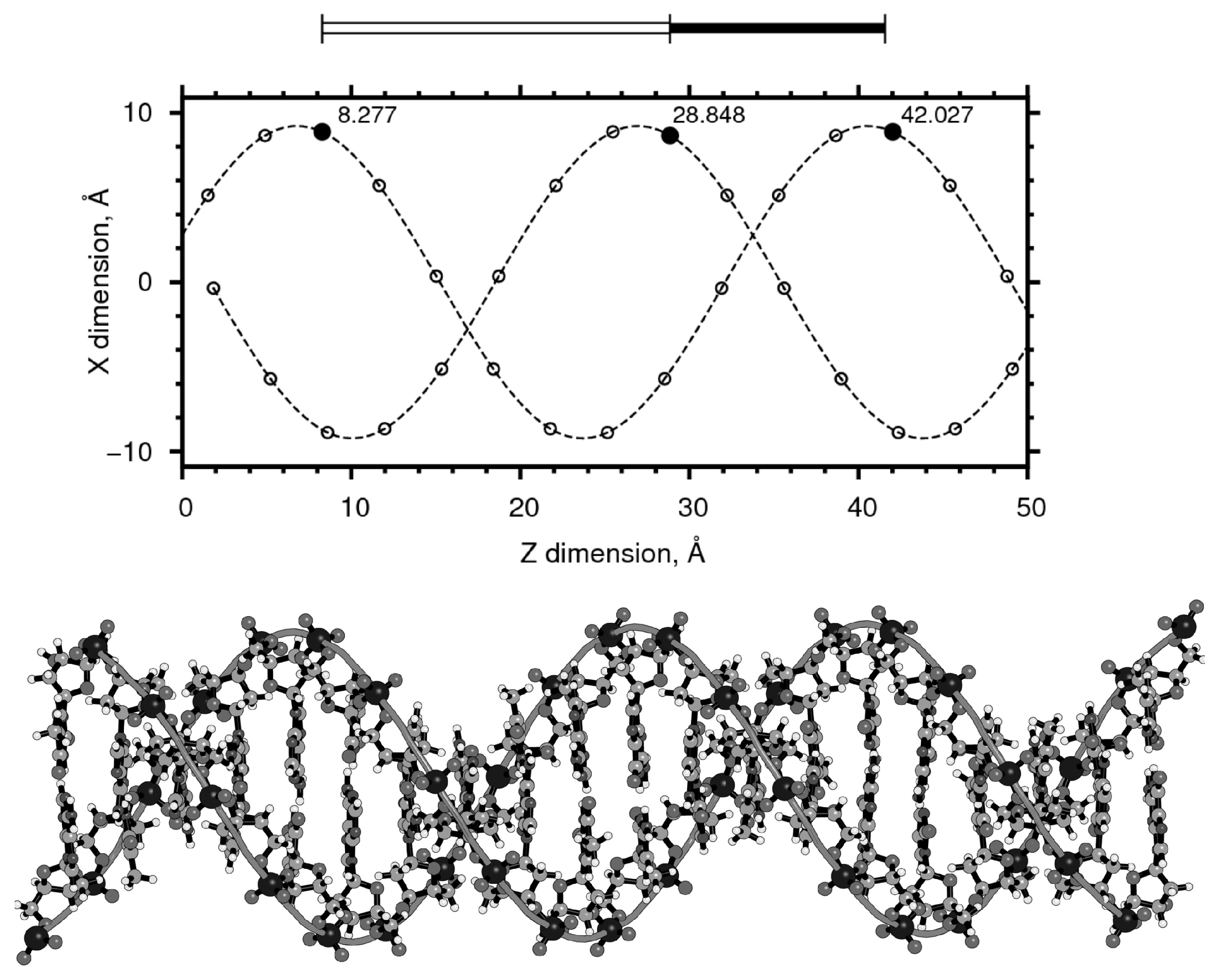
Anche il regno microscopico non è immune da queste regole. La molecola del DNA misura 34 angstrom di lunghezza per 21 angstrom di larghezza per ogni ciclo completo della sua spirale a doppia elica. Questi numeri, 34 e 21, sono numeri della serie di Fibonacci e il loro rapporto 1,6190476 si avvicina molto a Phi, 1,6180339.
Se hai trovato questo articolo interessante ringraziaci con un
Libri sull’argomento
[amazon bestseller=”sezione aurea” items=”6″ template=”table”]